3.16 Propiedades de la transformada inversa (linealidad y traslación).

3.16.1 Determinacion Trasformada Inversa Mediante Fracciones Parciales

3.15- Algunas Trasformadas Inversas

3.14- transformada inversa

3.13-Trasformada De Laplace Funcion Delta Dirac

Es evidente que, hasta el momento, la transformada de Laplace no es más que otra técnica para la resolución de ecuaciones diferenciales. Sin embargo, su popularidad (sobre todo en problemas de ingeniería) radica en que nos permite resolver ecuaciones en las cuales el término independiente puede ser sumamente "mal portado". En el caso de la ecuación (3), el término H(t) podría no ser una función continua (lo cual representa mejor a la realidad), con lo cual la función x(t) sería diferenciable por pedazos. El tipo de funciones H(t) que vamos a analizar son funciones que son nulas, excepto en algunos intervalos o instantes de tiempo predeterminados.

La función más simple de este tipo es la función escalón o función de Heaviside. Ésta se define para cualquier a = 0 como sigue:

3.12-Función delta de Dirac

FUNCIÓN DELTA DE DIRAC: En la práctica conviene trabajar con otro tipo de impulso unitario, con una “función” que aproxima y se define mediante el límite siguiente:

3.11- transformada de laplace de una funcion periodica

Si f(t) es una función periódica con período T:

 Ejemplos: Sobre la transformada de uns función periódica

Problema
Determine la transformada de la función cuya gráfica es:

SoluciónEsta función es periódica con período T=2 y para el cálculo de su transformada podemos utilizar la fórmula:



Puesto qur la función es seccionada en el intervalo [0,2] entonces la integral se calcula también por secciones:

asi:

por lo tanto



3.10- teorema de convulacion

establece que bajo determinadas circunstancias, la Transformada de Fourier de una convolución es el producto punto a punto de las transformadas. En otras palabras, la convolución en un dominio (por ejemplo el dominio temporal) es equivalente al producto punto a punto en el otro dominio (es decir dominio espectral).

Sean f y g dos funciones cuya convolución se expresa con F*G. (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo ). Sea F el operador de la transformada de Fourier, con lo que F[f] y F[g] son las transformadas de Fourier de f y g, respectivamente.

Entonces:



donde · indica producto punto. También puede afirmarse que:

Aplicando la transformada inversa de Fourier , podemos escribir:

3.9- transformada de integrales

Es cualquier transformada T aplicada sobre la función f(x) de la forma siguiente:

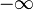La entrada de esta función T encontramos una función f(t), y la salida otra función F(u). Una transformada es un tipo especial de operador matemático. En ella t₁ y t₂ son dos valores que dependen de su definición, y pueden variar desde hasta .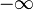

Hay numerosas transformadas integrales útiles. Cada una depende de la función K de dos variables escogida, llamada la función núcleo o kernel de la transformación.

Algunos núcleos tienen una K inversa asociada, K ^{− 1}(u,t) , que (más o menos) da una transformada inversa:

3.8- transformada de derivada

3.7-transformada de funciones multiplicativas

Ejemplo
Calcule

Solución
Aplicando el teorema anterior para , tenemos que

El siguiente ejemplo muestra una combinación del primer teorema de traslación y el teorema anterior.
Ejemplo
Calcule

Solución
Primero aplicamos el teorema de multiplicación por y luego el de traslación

Ejemplo
Calcule el valor de la siguiente integral

Solución
Por el teorema de multiplicación por , tenemos que

3.6- propiedades de la transformada de la place

linealidad:

derivacion:

integracion:

dualidad:

desplazamiento de frecuencia: